Tam giác là gì? Cách tính diện tích hình tam giác
Nội dung bài viết
Tam giác là một trong những hình học cơ bản được nghiên cứu rộng rãi trong toán học. Một trong những khái niệm quan trọng là diện tích hình tam giác - một đại lượng mô tả kích thước của hình học. Trong bài bài viết này, Viện đào tạo Vinacontrol sẽ giới thiệu về hình tam giác và công thức tính diện tích hình tam giác phổ biến cùng với một số lưu ý quan trọng khi tính diện tích tam giác. Ngoài ra, chúng tôi còn cung cấp "Bảng tính online diện tích các hình phẳng" để giúp bạn giải nhanh các bài tập tính diện tích.
1. Khái niệm hình tam giác
Tam giác hay hình tam giác là một loại hình cơ bản trong hình học: hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau.
Tam giác là đa giác có số cạnh ít nhất (3 cạnh). Tam giác luôn luôn là một đa giác đơn và luôn là một đa giác lồi (các góc trong luôn nhỏ hơn 180°). Một tam giác có các cạnh AB, BC và AC được ký hiệu là 

Khái niệm hình tam giác và công thức tính diện tích hình tam giác
2. Các đường trong hình tam giác
Đường cao là một đoạn thẳng đi qua một đỉnh và vuông góc với cạnh đối diện của đỉnh đó. Mỗi tam giác chỉ có ba đường cao. Ba đường cao của một tam giác đồng quy tại một điểm, điểm này được gọi là trực tâm của tam giác.

Giao của 3 đường cao là trực tâm của tam giác
Đường trung tuyến là một đoạn thẳng nối từ đỉnh đến trung điểm của cạnh đối diện. Một tam giác chỉ có ba đường trung tuyến. Ba đường trung tuyến của một tam giác đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.

Giao của 3 đường trung tuyến là trọng tâm của tam giác
Đường trung trực của một tam giác là đường vuông góc với một cạnh của tam giác đó tại trung điểm. Mỗi tam giác chỉ có ba đường trung trực. Ba đường trung trực của một tam giác đồng quy tại một điểm, điểm đó có tên gọi là tâm của đường tròn ngoại tiếp tam giác.

Giao của 3 đường trung trực là tâm của đường tròn ngoại tiếp tam giác
Đường phân giác là đoạn thẳng nối từ đỉnh đến cạnh đối diện và chia góc ở đỉnh làm 2 phần có số đo góc bằng nhau. Mỗi tam giác chỉ có ba đường phân giác. Ba đường này đồng quy tại một điểm. Điểm đó là tâm đường tròn nội tiếp tam giác

Giao của 3 đường phân giác là tâm của đường tròn nội tiếp tam giác
3. Các tính chất của hình tam giác
- Tổng các góc trong của một tam giác bằng 180° (định lý tổng ba góc trong của một tam giác).
- Độ dài mỗi cạnh lớn hơn hiệu độ dài hai cạnh kia và nhỏ hơn tổng độ dài của chúng (bất đẳng thức tam giác).
- Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn. Ngược lại, góc đối diện với cạnh lớn hơn là góc lớn hơn (quan hệ giữa cạnh và góc đối diện trong tam giác).
- Ba đường cao của tam giác cắt nhau tại một điểm được gọi là trực tâm của tam giác (đồng quy tam giác).
- Ba đường trung tuyến của tam giác cắt nhau tại một điểm. Điểm đó được gọi là trọng tâm của tam giác. Hay còn gọi là ba đường trung tuyến của tam giác đồng quy tại một điểm( đồng quy tại một điểm có nghĩa là cùng đi qua 1 điểm). Khoảng cách từ trọng tâm đến 3 đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó. Đường trung tuyến của tam giác chia tam giác thành hai phần có diện tích bằng nhau (đồng quy tam giác).
- Ba đường trung trực của tam giác cắt nhau tại một điểm là tâm đường tròn ngoại tiếp của tam giác (đồng quy tam giác).
- Ba đường phân giác trong của tam giác cắt nhau tại một điểm là tâm đường tròn nội tiếp của tam giác (đồng quy tam giác).
- Định lý hàm số cosin: Trong một tam giác, bình phương độ dài một cạnh bằng tổng bình phương độ dài hai canh còn lại trừ đi hai lần tích của độ dài hai cạnh ấy với cosin của góc xen giữa hai cạnh đó.
- Định lý hàm số sin: Trong một tam giác tỷ lệ giữa độ dài của mỗi cạnh với sin của góc đối diện là như nhau cho cả ba cạnh.
- Đường trung bình là đoạn thẳng nối trung điểm hai cạnh của tam giác; một tam giác có ba đường trung bình. Đường trung bình của tam giác thì song song với cạnh thứ ba và có độ dài bằng một nửa độ dài cạnh đó. Tam giác mới tạo bởi ba đường trung bình trong một tam giác thì nó đồng dạng với tam giác chủ của nó.
- Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành 2 đoạn thẳng tỷ lệ với 2 cạnh kề 2 đoạn thẳng đó.
4. Phân loại hình tam giác
Theo độ dài các cạnh
- Tam giác thường là tam giác cơ bản nhất, có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau. Tam giác thường cũng có thể bao gồm các trường hợp đặc biệt của tam giác.

Tam giác thường
- Tam giác cân là tam giác có hai cạnh bằng nhau, hai cạnh này được gọi là hai cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại gọi là góc ở đáy. Tính chất của tam giác cân là hai góc ở đáy thì bằng nhau.
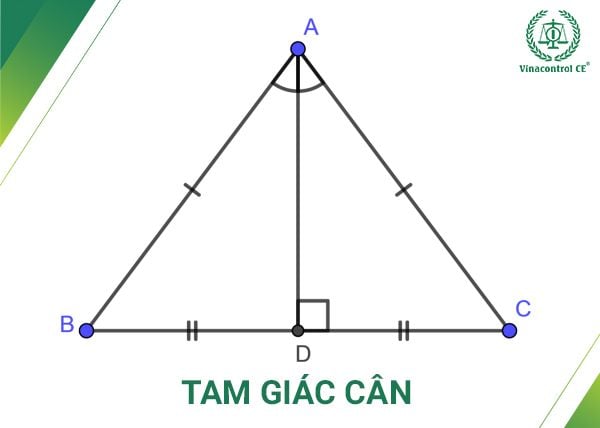
Tam giác cân
- Tam giác đều là trường hợp đặc biệt của tam giác cân có cả ba cạnh bằng nhau. Tính chất của tam giác đều là có 3 góc bằng nhau và bằng 60°.

Tam giác đều
Theo số đo các góc trong
- Tam giác vuông là tam giác có một góc bằng 90° (là góc vuông). Trong một tam giác vuông, cạnh đối diện với góc vuông gọi là cạnh huyền, là cạnh lớn nhất trong tam giác đó. Hai cạnh còn lại được gọi là cạnh góc vuông của tam giác vuông. Định lý Pythagoras là định lý nổi tiếng đối với hình tam giác vuông, mang tên nhà toán học lỗi lạc Pythagoras.

Tam giác vuông
- Tam giác tù là tam giác có một góc trong lớn hơn lớn hơn 90° (một góc tù) hay có một góc ngoài bé hơn 90° (một góc nhọn).

Tam giác tù
- Tam giác nhọn là tam giác có ba góc trong đều nhỏ hơn 90° (ba góc nhọn) hay có tất cả góc ngoài lớn hơn 90° (sáu góc tù)

Tam giác nhọn
- Tam giác vuông cân vừa là tam giác vuông, vừa là tam giác cân. Trong một tam giác vuông cân, hai cạnh góc vuông bằng nhau và mỗi góc nhọn bằng 45°.

Tam giác vuông cân
5. Công thức tính diện tích hình tam giác
5.1 Tính diện tích tam giác bằng cách sử dụng hình học
Diện tích hình tam giác được tính bằng tích của độ dài đáy nhân với chiều cao sau đó chia tất cả cho 2.
Hay nói cách khác, diện tích hình tam giác là 1/2 tích cạnh đáy và chiều cao. Đơn vị của diện tích hình tam giác là vuông, thường là cm2, dm2, m2,…
Công thức tính diện tích tam giác thường: S = ( a x h) /2
Trong đó: a là chiều dài đáy, h là chiều cao của tam giác (là đoạn thẳng hạ từ đỉnh xuống đáy đồng thời vuông góc với đáy của một tam giác), S là diện tích tam giác đó.

Công thức tính diện tích hình tam giác bằng sử dụng hình học
Công thức tính diện tích tam giác vuông: là 1/2 tích hai cạnh góc vuông hoặc 1/2 tích chiều cao và cạnh huyền.
Công thức tính diện tích tam giác cân, tam giác đều thì sẽ giống với cách tính diện tích tam giác thường.
5.2 Tính diện tích tam giác bằng cách sử dụng véc tơ
Nếu tứ giác ABDC là hình bình hành thì diện tích của nó được tính bởi công thức:
trong đó
![{\displaystyle [{\overrightarrow {AB}},{\overrightarrow {AC}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c932ca0c0c2ee04d5d9f706f966f72fd06c72cc) là tích có hướng của hai vectơ
là tích có hướng của hai vectơ  và
và  .
.Diện tích tam giác ABC bằng một nửa diện tích của hình bình hành ABDC nên:

Công thức tính diện tích hình tam giác bằng véc tơ
5.2 Tính diện tích tam giác bằng cách dùng lượng giác
Vì 


Công thức tính diện tích hình tam giác bằng lượng giác
6. Các dạng bài tập tính diện tích hình tam giác
Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao
Ví dụ 1: Tính diện tích tam giác thường và tam giác vuông có:
a) Độ dài đáy bằng 36cm và chiều cao bằng 21cm.
b) Hai cạnh góc vuông có độ dài lần lượt là 5dm và 6dm.
Bài làm
a) Diện tích hình tam giác là:
36 x 21 : 2 = 378 (cm2)
b) Diện tích hình tam giác là:
5 x 6 : 2 = 15 (dm2)
Đáp số: a) 378cm2
b) 15dm2
Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao
+ Từ công thức tính diện tích, ta suy ra công thức tính độ dài đáy: a = S x 2 : h
Ví dụ 1: Tính độ dài cạnh đáy của hình tam giác có chiều cao bằng 60cm và diện tích bằng 4500cm2.
Bài làm
Độ dài cạnh đáy của hình tam giác là:
4500 x 2 : 60 = 150 (cm)
Đáp số: 150cm
Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy
+ Từ công thức tính diện tích, ta suy ra công thức tính chiều cao: h = S x 2 : a
Ví dụ 1: Tính chiều cao của hình tam giác có độ dài cạnh đáy bằng 50cm và diện tích bằng 1125cm2.
Bài làm
Chiều cao của hình tam giác là:
1125 x 2 : 50 = 45 (cm)
Đáp số: 45cm
Tổng kết, trong bài viết này đã giúp bạn hiểu sâu hơn về hình tam giác và các tính chất của nó. Bên cạnh đó, bài viết còn cung cấp 3 công thức tính diện tích hình tam giác. Mong rằng các thông tin trên sẽ hữu ích với bạn.
Ngoài bạn, bạn có thể tham khảo thêm các kiến thức hữu ích dưới đây:
✍ Xem thêm: Bảng quy các đổi đơn vị đo độ dài đầy đủ
✍ Xem thêm: Quy đổi đơn vị đo khối lượng trực tuyến, dễ dàng
✍ Xem thêm: Chuyển đổi đơn vị đo diện tích dễ dàng với 1 cú nhấp chuột
✍ Xem thêm: Tính diện tích hình vuông | Bài tập có lời giải
✍ Xem thêm: Công thức tính diện tích hình thoi và cách giải bài tập chi tiết

![{\displaystyle S_{ABCD}=|[{\overrightarrow {AB}},{\overrightarrow {AC}}]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdcc1ce1c5e73f7e204ca7e1a3377e5d99127ea8)
![{\displaystyle \lg {\check {a}}S_{ABC}={\frac {1}{2}}|[{\overrightarrow {AB}},{\overrightarrow {AC}}]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d948f0ec78765064b48246ba1c2c0fda34a452e0)


